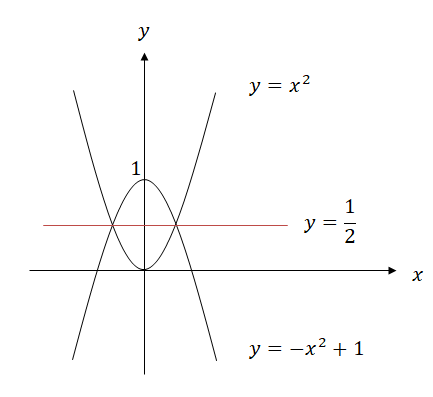
y = f(x) ∧ y = g(x) ⇒ 2y = f(x) + g(x)
Example:
y = x² ∧ y = -x² + 1 ⇒ y = 1/2
cf.
[i]
y = f(x) ∧ y = g(x) ⇔ 2y = f(x) + g(x) ∧ 0 = f(x) - g(x)
[ii]
f(x,y) = 0 ∧ f(y,x) = 0 ⇔ f(x,y) + f(y,x) = 0 ∧ f(x,y) - f(y,x) = 0
[iii]
f(x,y)=0 ∧ g(x,y)=0 ⇒ ∃k ( f(x,y) + kg(x,y)=0 )
[iv]
f(x,y)=0 ∧ g(x,y)=0 ⇔ ∀k ( f(x,y) + kg(x,y)=0 )
[v]
y=ax²+bx+c ∧ y=px²+qx+r ⇒ (p-a)y=(pb-aq)x+(pc-ar)
[vi]
x²+y²+ax+by+c=0 ∧ x²+y²+px+qy+r=0 ⇒ (a-p)x+(b-q)y+(c-r)=0
