Lorentz transformation

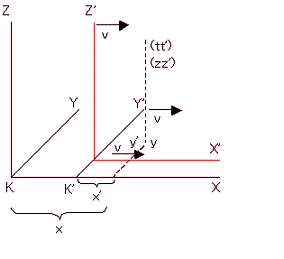
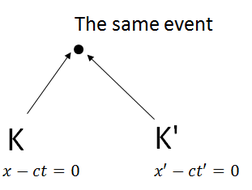
From the mathematical point of view,

x'-ct' = λ(x-ct) ・・・(1),

x'+ct' = μ(x+ct)・・・(2),

and λ, μ = const.

hold.

 

Using a = (λ+μ)/2, b = (λ-μ)/2,

(1) and (2) can be written as

x' = ax - bct   ・・・(3)

ct' = act - bx   ・・・(4)

 

x' = 0 and (3) ⇒ x =bct/a

Also, dx/dt = bc/a = v ・・・(5), which is the relative velocity.

 

t=0, x'=0, and (3) ⇒ x=0

t=0, x'=1, and (3) ⇒ x = 1/a

Therefore Δx = 1/a.

 

On the other hand,

t'=0, x=0, (3) and (4) ⇒ x'=0

t'=0, x=1, (3) and (4) ⇒ x'=a(1-b^2/a^2) = a(1-v^2/c^2)

Therefore Δx' = a(1-v^2/c^2).

 

Followed by the principle of relativity,

Δx = Δx'.

Therefore  a^2 = 1/(1-v^2/c^2) ・・・(6).

 

By (5) and (6),

(a,b) = (1/√1-v^2/c^2, v/c 1/√1-v^2/c^2) or

            (-1/√1-v^2/c^2, -v/c 1/√1-v^2/c^2).

 

As v → 0, x = x' = 0 and t = t' = 0 (K=K'), then 

(a,b) = (1/√1-v^2/c^2, v/c 1/√1-v^2/c^2) is valid.

 

Therefore Lorentz transformation are

   x' = (x-vt)/√1-v^2/c^2

   t' = (t - v/c^2 x)/√1-v^2/c^2