
given the point A(u,v) and the line y=ax+b,
find the point B(p,q) which is symmetrical with respect to A.
the middle point between A and B is
((u+p)/2, (v+q)/2), and the point satisfies the line y=ax+b, so we get
(v+q)/2 = a*(u+p)/2 + b ⇔ ap - q = v - au - 2b ・・・(Σ)
|AC| = |BC| then we get
root(u^2+(v-b)^2) = root(p^2+(q-b)^2) ・・・(Λ)
solving (Σ) and (Λ) for p and q
(subject to a^2+1!=0,) we get
p =
-a^2 u - 2ab + 2av + u
--------------------------------
a^2+1
q =
a^2 v + 2au + 2b - v
---------------------------
a^2+1
question
when y=3x+2, A(1,7), find the point B(p,q).
p =
-2×3×2+1-3^2×1+2×3×7
-------------------------------- = 11/5
3^2+1
q =
2×2+2×3×1-7+3^2×7
--------------------------- = 33/5
3^2+1
the formulas of p and q are complex, so
you do not have to remember them.
all you have to do is to find the two equations,
v+7 u+1
---- = 3 *------ + 2 ⇔ v = 3u
2 2
and
u^2 +(v-2)^2 = 26, and you solve them.
other solutions
finding the line through B(p,q) that is vertical to the line y=ax+b,
that is q = -1/a (p-u) + b (a=!0).
solving this and (Σ) above allows you to find the point (p,q).
or
if you can find the two lines m and n, you can get the answer by solving them.
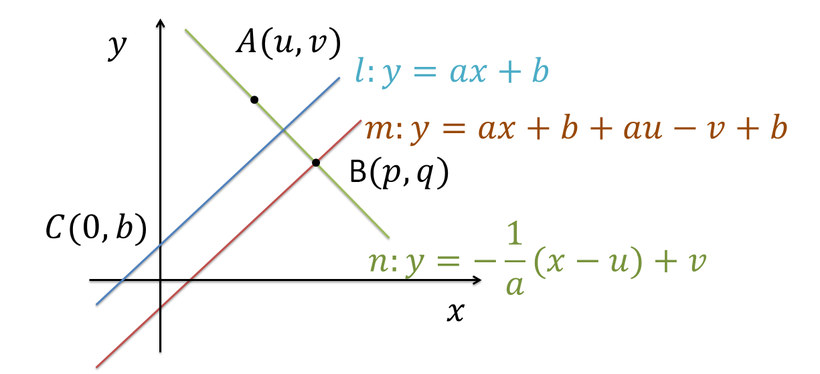

Write a comment