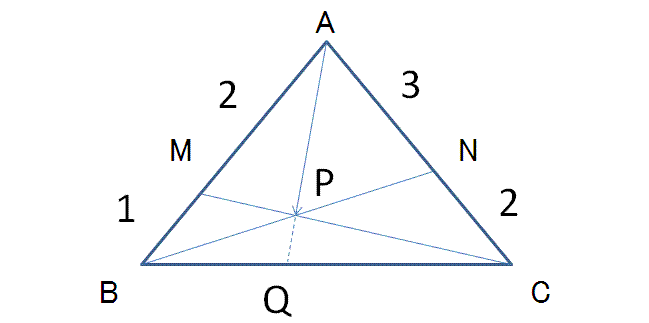
AP

= sAB + (1-s)AN = sAB + (1-s)AC * 3/5 ・・・(1)

= tAM + (1-t)AC  = tAB * 2/3 + (1-t)AC・・・(2)

where s and t are parameters.

  

comparing coefficients of (1) and (2) expressions,

(AB and AC are linearly independence)

           s = t*2/3 and

    (1-s)*3/5= 1-t

solving these equations,

           s = 4/9

            t = 2/3

substituting s = 4/9 into the expression (1),

    AP = 4/9*AB + 1/3*AC

AQ 

= uAB + (1-u)AC ・・・(a)

= vAP 

= 4v/9*AB +  v/3*AC・・・(b)

comparing coefficietns of (a) and (b),

        u = 4v/9 and

      1-u = v/3

solving these equations,

        u = 4/7,

        v = 9/7

substituting u = 4/7 into the expression (a),

    AQ = 4/7*AB + 3/7*AC

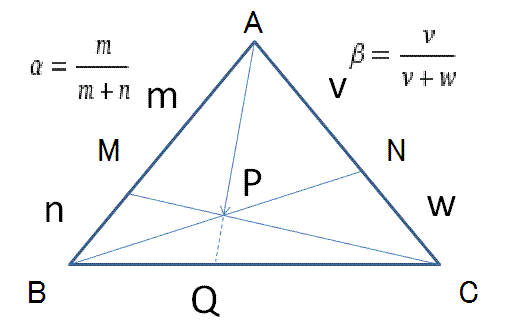
let AB and AC be AB !// AC ∧ AB!=0 ∧ AC!=0.

AP

= sAB + (1-s)AN = sAB + (1-s)AC * β

= tAM + (1-t)AC  = tAB * α + (1-t)AC

 

comparing coefficients of these two expressions,

           s   = tα and

    (1-s)β  = 1-t

solving these equations,

           s = (α-αβ)/(1-αβ)

            t = (1-β)/(1-αβ)

 

AP = 

　　　(α-αβ)         (β-αβ)

　　　------- AB + ------- AC

       (1-αβ)         (1-αβ)