31. March 2015

central limit theorem

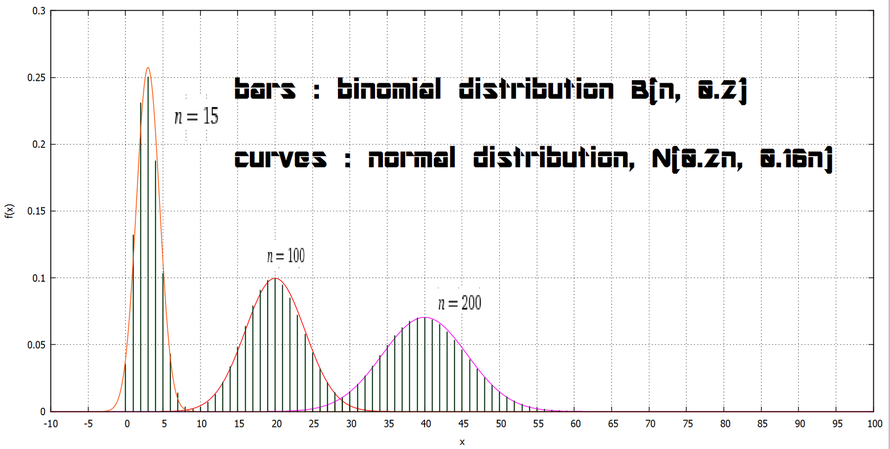
fig.1 : in general, as n is larger, the binomial distribution is more similar to the normal distribution. by the way, even when n = 15, the binomial distributions already seem to fit the corresponding normal distributions well.
fig.1 : in general, as n is larger, the binomial distribution is more similar to the normal distribution. by the way, even when n = 15, the binomial distributions already seem to fit the corresponding normal distributions well.

for binomial distribution, B(n, p), defining Z = (X - μ)/σ, as n is tended to infinity, 

the Z distribution approaches normal distribution, N(0, 1).


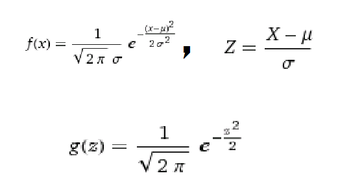
<Q> 

the Capacities of 300 canned drinks almost obey normal distribution. the mean value is 199.3 g, the standard deviation 6.0 g.

What is the capacity of the 100th canned drink counting on from the larger number?

 

<A>

int_u^inf f(x) dx

by applying Z = (X - 199.3)/6.0

= int_v^inf g(z) dz = 1/3

 

finding v such that int_v^inf g(z) dz = 1/3,

v is 0.43 using normal distribution table.

 

solving (X - 199.3)/6.0 = 0.43 for X,

X = 201.88 (g)

Tags: math

Write a comment

Comments: 0