surface integral

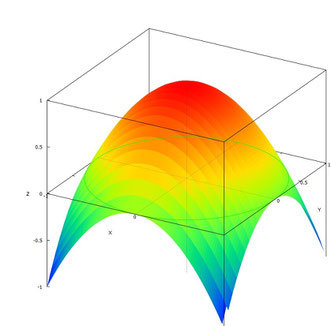
for a surface S: z=1-x^2-y^2 (z>=0), 

calculate int(S) dS.

 

setting φ = x^2+y^2+z-1 = 0,

dS = |∇φ|dxdy

     = root(4x^2+4y^2+1)

therefore, 

int(D) root(4x^2+4y^2+1) dxdy

(D={(x,y)|x^2+y^2<=1})

 

using x = rcosθ, y = rsinθ,

 

int_(0)^(2pi) dθ int_0^1 root(1+4r^2) r dr

=  1/6 (5 sqrt(5)-1) pi~5.33